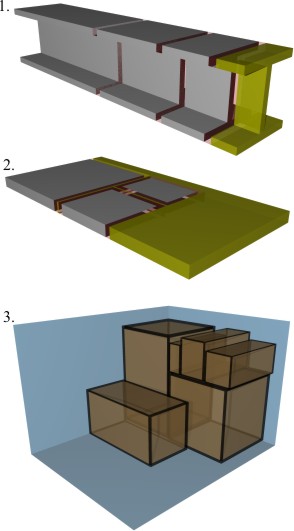
Nesting algorithm

Nesting algorithms are used to make the most efficient use of material or space by evaluating many different possible combinations via recursion.

Linear (1-dimensional) The simplest of the algorithms illustrated here. For an existing set there is only one position where a new cut can be placed--at the end of the last cut. Validation of a combination involves a simple Stock - Yield - Kerf = Scrap calculation.

Plate (2-dimensional) These algorithms are significantly more complex. For an existing set, there may be as many as eight positions where a new cut may be introduced next to each existing cut, and if the new cut is not perfectly square then different rotations may need to be checked. Validation of a potential combination involves checking for intersections between two-dimensional objects.

Packing (3-dimensional) These algorithms are the most complex illustrated here due to the larger number of possible combinations. Validation of a potential combination involves checking for intersections between three-dimensional objects.