Linear temporal logic

Linear temporal logic (LTL) is a modal temporal logic with modalities referring to time. In LTL, one can encode formulae about the future of paths such as that a condition will be eventually be true, that a condition will be true until another fact becomes true, etc.

Syntax

LTL is built up from a set of proposition variables $p_{1},p_{2},...$ , the usual logic connectives $\neg ,\lor ,\land ,\rightarrow$ and the following temporal modal operators:

N for next;
G for always;
F for eventually;
U for until;
R for release.

The first three operators are unary, so that N $\phi$ is a well-formed formula whenever $\phi$ is a well-formed formula. The last two operators are binary, so that $\phi$ U $\psi$ is a well-formed formula whenever $\phi$ and $\psi$ are well-formed formulas.

Semantics

An LTL formula can be evaluated over a sequence of truth evaluations and a position on that path. An LTL formula is satisfied by a path if and only if it is satisfied for position 0 on that path. The semantics for the modal operators is given as follows.

Textual	Symbolic	Explanation
Unary operators:
N $\phi$	$\circ \phi$	Next: $\phi$ has to hold at the next state. (X is used synonymously.)
G $\phi$	$\Box \phi$	Globally: $\phi$ has to hold on the entire subsequent path.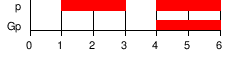
F $\phi$	$\Diamond \phi$	Finally: $\phi$ eventually has to hold (somewhere on the subsequent path).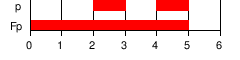
Binary operators:
$\phi$ U $\psi$	$\phi ~{\mathcal {U}}~\psi$	Until: $\psi$ holds at the current or a future position, and $\phi$ has to hold until that position. At that position $\phi$ does not have to hold any more.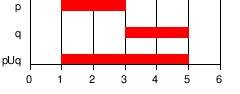
$\phi$ R $\psi$	$\phi ~{\mathcal {R}}~\psi$	Release: $\phi$ releases $\psi$ if $\psi$ is true until the first position in which $\phi$ is true (or forever if such a position does not exist).