Milne model

Milne’s Model of the Universe

A Comparitive Description

(see Edward Arthur Milne)

The Three Cosmological Models

Overall, there are three distinct classifications for cosmological models which have been seriously considered. These are the steady-state model, the standard cosmological model, and the Milne model.

Briefly the three models can be described as follows:

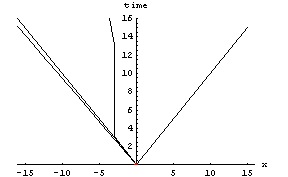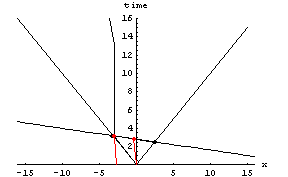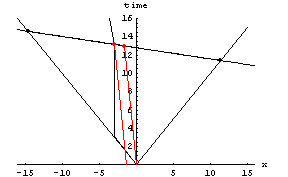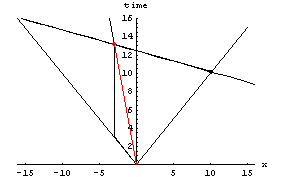
The Milne Model: an infinite explosion that took place at a point in space at an instant in time, expanding into pre-existing space.

The Standard Cosmological Model (SCM): a static universe, where space is constantly expanding in a manner consistent with Einstein’s Field Equations.

The Steady-State Universe: (Hoyle?) A universe of infinite age and size where matter may be disappearing and reappearing over time.

This article focuses on the first two, though the third certainly deserves consideration as well.

Philosophical Differences

The differences between Milne’s concept of space-time and Einstein’s concept of space-time appear to run much deeper than is commonly appreciated. Reading treatments of the Standard Cosmological Model written by respected physicists of today lead to bewilderment. For instance it is in fashion to comfort the layperson by explaining that the big bang was not actually an explosion, but simply the expansion of space. This is completely at odds with the cosmology of Milne which is represented exactly by an explosion of matter into space.

The Scale Factor

The central question of the Standard Cosmological Model is to determine the scale factor of the universe, whether it be constant or varying, and thus determine the “shape” of space.

In contrast, Milne denies that space has a shape or a scale factor which can be measured or observed. In this respect, Milne and Einstein had an immense philosophical gulf between them.

Ironically, in developing his arguments against Einstein’s concept, Milne put together the mathematics which were later adopted to create the Standard Cosmological model.

Philosophical Conundrum, Is Space Possible Without Matter?

Einstein said that space without matter was impossible, while Milne’s model takes as a premise the existence of a Euclidian coordinate system pre-existing the Big Bang. This may be the root conflict between the two models.

A diagram of the Milne Model universe clearly shows white-space beyond the edge of a sphere, representing space *outside* the universe. This marks Milne’s model as being clearly distinct from any popular cosmology today.

An oft-made assumption is that space cannot exist without matter, and with this reasoning, the possibility of Milne’s model is eliminated, leaving the standard cosmological model as the next most likely possibility.

However, some might argue, contrary to Einstein, that space, or at least a coordinate system, could exist without matter (or in a region of space beyond all matter of the universe), in which case Milne’s Model becomes a contender. There seems to be no difficulty in describing such a space, or conceptualizing such a space, but the SCM holds as self-evident that space only exists between all things. By having a diagram of a model of the universe which explicitly represents the space beyond all matter of the universe, he may have convinced other scientists of his time that he was crackers.

However, Milne’s model should be considered, because many of the great mysteries currently under research in cosmology can be explained without difficulty by using Milne’s model. These include the Cosmic Background Radiation, Inflation, and Galactic Superstructure. Milne did not, himself, delve deeply into these concepts, as he was more focused on other features and more challenging problems of his model which I have not even yet considered.

A Note on the Two Scale Factors (General vs. Special Relativity)

The concept of a scale factor based on the position of the observer is not the same as the concept of a scale based on the observer’s velocity.

Milne did not admit the existence of a scale factor based on the position of the observer, but he did accept the validity of the Lorentz Transformation equations which scale the distance between two events according to the observer's velocity.

A Note on Homogeneity

Sections 60-64 of Relativity, Gravitation and World Structure present a masterful critique of the Standard Cosmological Model. In approximately five pages, Milne very politely points out that in general, in a “system homogeneous according to” … “the methods of current relativistic cosmology” … “observers O and O’ will not recognize, or analyze, the system open to their observations as homogeneous.”

Milne was not critical of the use of the definition of homogeneity used by cosmologists but cautioned strongly against its use as a cosmological principle. “This conventional homogeneity is only definite when the motion of the particles is first prescribed.” His alarmed but polite arguments continue throughout section 62, and in section 63, he states explicitly, that homogeneity has been shown to break down, then goes on to prove this in section 64.

However, his proof in section 64 uses relatively moving observers. But by assuming the expansion of space instead of relative motion, the standard cosmological model was wily enough to duck his excellent arguments.

However, in section 60, he points out that a static universe is necessarily part of a favored reference frame, and fails to satisfy another equally valid cosmological principle. Perhaps the expansion of space allows the SCM to be neither static nor have particles in relative motion, and thus the proponents of this idea have their cake and eat it too. However, I think this cake is very flaky.

Strangely, Milne is sometimes given credit for discovering that the Principle of Relativity is actually homogeneity. Which is odd since he repeatedly says the idea of homogeneity breaks down or has been disproven in "Relativity, Gravitation, and World Structure."

However, if you dismiss, out of hand, the model that Milne was *actually* trying to present, as most cosmologists do, then the only remaining possibility is the one described below, which is static and homogeneous.

Self-Consistent Assumptions of the Standard Cosmological Model

Descriptions of the SCM vary. Some theorists won't hold to the ideas that follow, and some may say that I am presenting something besides the 'standard model'. I wish to present just one version of the Standard Cosmological Model which represents almost exactly the opposite view of A. E. Milne's Model, so as best to highlight the differences. I would welcome input that clarifies the Standard Model.

The following model represents what I have heard from many sources, and a careful reading of Milne leaves the model with the following properties more-or-less unscathed by any self-consistency violations. Self-consistency is a bare minimum criterion for a good mathematical model. A good physical theory should also be consistent with observations, and that question will be put off for a few moments under the heading "Shortcomings."

Here is a list of some of the properties of the Standard Cosmological Model which is most opposite Milne's Model in virtually every way, yet still describes a self consistent model of the universe:

1. The universe has roughly the same density throughout (if you make your scale coarse enough, say kilograms/cubic mega-parsec), though this density decreases over time due to the expansion of space.

2. The red-shift of distant galaxies is due to the expansion of space instead of the recession velocity of the galaxies.

3. Because distant galaxies actually have no relative velocity, they are in the same reference frame, and thus no Lorentz Transformation is required to convert between the coordinates of the observers on these galaxies.

4. Because no Lorentz Transformation is required, time can be considered to be a universal, or absolute, quantity.

5. Because no Lorentz Transformation is required, Special Relativity can be considered valid, though it does not apply to any arguments in cosmology, rendering it true but impotent.

6. The SCM assumes Einstein's Field Equations; differential equations with boundary conditions. Unfortunately these are described in terms of rather complicated differential equations of 10 X 10 matrices, so each term could be represent as many as 100 numbers. If you feel overwhelmed by this, remember that those who did not understand Ptolemy's epicycles were once discouraged from studying astronomy.

7. The solution to the Einstein Field Equations was given by Friedmann, which has not been translated into English, to my knowledgae. The curvature of the scale of space may be negative, positive, or zero, and Friedmann's solution also contains an extra constant, called the cosmological constant. Apparently the boundary conditions for this problem have not been determined, or we should be able to determine the constants. The current procedure of identifying Bessel coefficients for the Cosmic Background Radiation is an example of astronomers trying to find these boundary conditions to get more explicit values for the constants of the Friedmann Solution.

The Standard Cosmological Model has successfully described a plausible possibility for a universe which does not require the use of Special Relativity and the Lorentz Transformations on the cosmological scale. It accepts the legitimacy of Special Relativity, but only in applications at a local level.

One benefit of all this is that absolute time becomes a possibility. The Special Theory of Relativity threatens damage to our human sensibilities of time and space if taken at face value as a universal law.

Due to its apparent self-consistency, the SCM is worthy of study at least as a philosophical pursuit, and if gravity waves, dark matter, dark energy, or any of the other conjectured necessary ingredients of the SCM are discovered, these would be discoveries of profound importance—our ability to harness such resources could give us infinite mobility to explore our universe and return home before dinner. So I certainly don’t want to discourage research in this direction. Even if there is only a 1 in a million chance that the SCM is correct, no time spent searching for these things should be considered wasted.

Even so, the SCM exists mainly in the Sherlock Holmes sense that having eliminated the impossible, whatever else is left, however improbable, must be the truth. However, Milne, himself presented a much more probable scenario in 1933, where the Special Theory of Relativity applies everywhere. Milne's model has been underemphasized for the last 70 years.

Milne Model

I hardly think it would do any harm for the student of cosmology to consider the Milne model of the universe.

Milne’s model describes

1. A literal explosion of matter from a point into pre-existing space. It seems that this presence of pre-existing space is part of what gives modern cosmologists fits.

2. But in the Milne model, space is considered to have no properties, so this model has no use for the concept of a scale factor, and thus the Friedmann metric does not apply. (There is no positive, negative, or even zero curvature of space, and certainly no cosmological constant in Milne's model.)

3. The red-shift of galaxies is caused almost entirely by recession velocity. (The slowing of time near gravitational sources also causes a redshift of light from massive objects, but this is a change in the speed of time--not the scale of space.)

4. Simultaneity, as perceived by relatively moving observers, is completely determined by using the Lorentz Transformation to convert between Euclidian coordinate systems of the different observers.

5. The density of the universe which corresponds to the cosmological principle of “no preferred reference frame” is a fully determined function. And as it happens, and as Milne expected, the mass and number of particles in this universe must be infinite in order to correspond to this function.

6. The universe is an expanding sphere with infinite density on the outer surface, in the reference frame of any observer within it.

7. (Any hypothetical observer outside will never see it until it’s too late, since it’s infinitely dense outer surface is moving at the speed of light in all reference frames.)

In fact, I cannot iterate every difference between Milne’s Model and the Standard Cosmological Model. I only know that virtually every implicit assumption made by modern cosmologists must be re-evaluated in order to simply begin consideration of the Milne model.

The Problems of Modern Cosmology

Astronomers would like to have some manner of predicting things so they can point their telescopes toward regions which should have interesting things to look at. However, the best the Standard Cosmological Model has had to offer is to say "That's weird; I wonder what in the world causes that?"

A good example of this is the discovery by Penzias and Wilson of the Cosmic Microwave Background Radiation. Soon after their discovery, Robert Dicke called them up, and shortly thereafter he published a "prediction" of what had already been discovered.

Milne, on the other hand, predicted a Cosmic Background in 1933, long before it had actually been discovered, which you can verify for yourself by reading his books.

What other grand predictions of astronomical nature has the standard cosmological model given us? I leave the answer to that question for other contributors to fill in, because I don't know.

Instead of predictions, we have a list of unexplained phenomena--observations that took the cosmologists by surprise for which they struggle to find reasonable answers.

John Baez has provided an extensive list of shortcomings of standard cosmology. http://www.damtp.cam.ac.uk/user/gr/public/bb_problems.html

These include the flatness problem, the horizon problem, the density fluctuation problem, the dark matter problem, the exotic relics problem, the thermal state problem, the cosmological constant problem, the singularity problem The timescale problem,

Exactly how many outstanding problems and unexplained phenomena one should expect with a model of the universe, I am not sure, but nine seems a little high.

A Suggested Approach to Each Problem Using Milne's Model

Some of the shortcomings of SCM simply disappear with Milne’s model. Some require a little more explanation, and some of them switch from being questions of cosmology and become questions entirely about the very nature of matter itself.

The Flatness Problem

Assuming the SCM, observations of the universe indicate that the speed of the stretching of space is slowing asymptotically toward zero. The Milne Model’s assumption of space without a scale factor makes this problem meaningless. In Milne’s model the question must be asked in a different way.

The relation between the distance of a nebula and its velocity in Milne’s model is simply

  Distance = Velocity * Time.  

The distance equals rate times time equation is familiar to algebra and physics students at all levels. The SCM uses another equation to address the motion of galaxies in the universe, known as the Friedmann solution to Einstein’s Field Equations. See Robertson-Walker coordinates. In fact mathematical similarities between Milne's Model and the "negative curvature" version of

It may be surprising for many readers to learn that this equation has been replaced in modern cosmology with an equation called the Friedmann Solution to Einstein's Field Equations.

However, Milne did not preclude the possibility of acceleration after the beginning of time, so, in such cases where some acceleration occurred after the Big Bang.

  Distance = Velocity * Time + Initial Distance, 

Naturally, since it has been a very long time since the last such acceleration, the local objects are moving very slowly, and the objects which are moving quickly are so far away that we barely notice them. The universe, in Milne’s model shows no signs of slowing down whatsoever, and never would have been expected to.

The Horizon Problem

The Horizon Problem is a question of why the cosmic background is so smooth. Implicit in the Horizon problem is the assumption that the initial size of the universe is nonzero. This would allow the possibility of objects which were noncausally connected. It would also allow the possibility that distant stars and galaxies would simply wink into existence as the light from them first reached us from the distance. This may be a common concept of the cause of the cosmic background.

Milne’s model assumes that the universe’s initial size was exactly zero, and therefore there are no objects in the universe that are not causally connected in some way. They were all touching at the moment of the big bang.

The Dark Matter Problem

The Dark Matter Problem has been presented in two main ways. One is to question why the outer arms of spiral galaxies have the same velocity as the inner arms. It has been determined that 90% of the matter in these arms cannot be seen, and is thus “dark matter.” This is easily explained by the presence of meteors, planets, dust, and gas which of course does not glow and thus cannot be seen from here.

The other manner in which the Dark Matter Problem has been presented is as the question of what matter is present to warp the space in a manner consistent with the assumptions of the standard cosmological model and the observations of reality. A much larger amount of matter is necessary for this. The most conservative description of this matter has been described as huge clouds of neutrinos, or some other neutral particle with much higher mass than neutrinos.

So the standard cosmological model requires large amounts of mundane dark matter and enormous amounts of mysterious dark matter in order to make the model consistent with observations.

The Milne model on the other hand, requires large amounts of mundane dark matter (to explain the spiral arm motion), but does not require enormous amounts of mysterious dark matter. I would go so far as to say that Milne’s model predicts large amounts of Mundane dark matter, as the equation he gives for the density of the universe is an equation of fluid dynamics, which would indicate a large number of tiny particles. Stars and galaxies would represent blemishes and concentrations among an otherwise smooth fluid. (I am tempted to use the word homogeneous here, but this smooth fluid has a finite density at the center and an infinite density at the edges.)

Which brings us to:

The Density Fluctuation Problem

Why are there blemishes and concentrations of matter in the universe? “The perturbations which gravitationally collapsed to form galaxies must have been primordial in origin; from whence did they arise?”

Astronomers have noticed that the visible matter of the universe has organized itself into perturbations known as stars, galaxies, clusters, and super clusters. In fact, these super clusters seem to appear in great long swaths across the cosmos such as the Shapley Concentration, (AKA the Finger of God).

Many opinions are out there as to the nature of the cause of these perturbations. Some have suggested that they appear due to superstrings; monofilament remnant leftovers of the big bang, with the gravitational strength of black holes or neutron stars. Others have suggested that the phenomena are due to some kind of crystal defect in the homogeneity of the universe.

Another option is that a large mass passed through the region while it was still dense and just as a fast moving boat creates whirlpools on the surface of a smooth pond, so did this large mass leave spiral galaxies forming in its wake. As unbelievable as it may sound, this is consistent with Milne’s model.

The Inflation Problem

I have been informed that Inflation is the theory which explains many, if not all of the outstanding questions of the SCM. Interestingly, it is also viewed as a “problem.” There is no question that inflation is observed, the only question is by what mechanism it occurs.

The challenge for proponents of the SCM is to explain inflation in a manner which does not invoke the Lorentz Transformations. These efforts remind me of the labors of Ptolemy, using the theory of “epicycles” in order to explain the observed retrograde motion of planets while insisting that the earth was the only valid reference frame. A brilliant scientist such as Ptolemy can put together a self-consistent model even under circumstances where the initial assumptions are flawed. Humans were very attached to absolute space and they did not give it up easily. The Standard Cosmological Model will eventually be viewed as a similar struggle to hold onto absolute time.

Milne’s model, on the other hand, does invoke the Lorentz Transformations, and thus provides a mechanism for inflation with no difficulty. The model inflates with respect to any observer who undergoes acceleration, in a simple manner described by putting it through a Lorentz Transformation about an event which is not the origin.

The first of these two images shows a two dimensional cross-section of the space of a large mass in its own reference frame. The second of the two animations shows the Minkowski Space-time diagram showing the path of this object, as well as its line of simultaneity at each moment, and the red dot which represents the stationary center of the universe from its perspective.

If a body were to be accelerated by Brownian Motion in the thermodynamics of the hot big bang, it would be moved to a new reference frame, where instead of seeing itself at the center (and least dense section) of very small universe, it would see itself at the very dense edge of a vast universe. The objects coming from the center of that universe would be approaching it at an alarming rate. If the mass of this body were large enough (which is highly likely if it came from the first fraction of a second... see The Singularity Problem, below), it would leave condensed matter and spiral galaxies in its wake.

The Exotic Relics Problem

“Phase transitions in the early universe inevitably give rise to topological defects, such as monopoles, and exotic particles. Why don't we see them today?”

Most of these phenomena would be blocked from view by the layer of newly formed Hydrogen atoms at the visible inner surface of the sphere of Milne’s Model. This is fairly well explained by the concept of “the surface of last scattering” although using the Milne model would give an even greater understanding of why this surface was so incredibly effective at blocking everything except for those photons unable to knock an electron out of the 1S orbital of a hydrogen atom.

The Thermal State Problem

Again, the question of why the universe began in a state of thermal equilibrium implicitly assumes the initial size of the universe was nonzero. This seems to be more of an argument against the Steady State model than the Standard Cosmological Model. And regardless, it doesn't apply to Milne's Model, because everything was in thermal contact at the first instant.

The Cosmological Constant Problem

Milne’s model does not admit the validity of Einstein’s Field Equations, the scale factor, or the Friedmann solutions. The cosmological constant problem in Milne's model is that anyone with a solid grasp of Milne's model well in mind will be unable to find any conceptual use for the Friedmann Solution, and no matter how strong his interest in the subject, he will be dismissed by some cosmologists as unteachable.

The Singularity Problem

This is an important problem but it is not compatible with the Thermal State Problem or the Horizon Problem, since both of them implicitly assume an initial nonzero size of the universe. Supporters of the Steady-State model do not need to worry about the singularity problem, but it is probably the most important problem of the Milne Model.

The Milne model requires the entire system to occupy a single point at first instant. (Why? Because application of the Lorentz Transformation to two simultaneous noncoincidental (nontouching) events causes them to become nonsimultaneous and these two events may be separated by appropriate LT's to any arbitrary separation in time and space. This therefore would fall under the realm of a steady-state model.)

Since the distance between any two particles is zero at this instant, this requires, by the Heisenberg Uncertainty Principle, (HUP) that either the relative momentum between any two particles in the system be infinite, or Planck's constant is reduced to zero. Assuming the former, this can be accomplished in either of two ways, which are setting the mass of the particle to infinity, or by setting its velocity to the speed of light.

Milne’s model does not eliminate the singularity problem, though I think research of this problem could be more fruitful if Milne’s model were considered. One element I have noticed is that statistical thermodynamics and solid-state mechanics usually consider systems with an equipartition of momentum. A careful analysis of the Milne model will show that the Lorentz invariant distribution he describes is an equipartition of rapidity, which is a fundamentally different quantity.

The Timescale Problem

Milne’s approach to cosmology is to answer the question of the time-scale problem before any other question is pursued. Every detail of his analysis is defined from the perspective of one observer and his or her clock. He defines two different timescales: proper time and coordinate time. Coordinate time being the time that an observer would measure across the whole of the universe as being the plane of simultaneity described by Lorentz transformation equations, and proper time being the age of an object which has a definite meaning only at the event where it is described. The standard cosmological model was developed by taking his proper time measurements and pretending that they can be set equal across the universe. So yes, there is a timescale problem with the Standard Cosmological Model. A glaring one which Arthur Milne attempted to fix in 1933, but apparently was misunderstood and misrepresented.

Sources

The tradition in books on relativity theory in making the transition from the Special Theory to the General Theory is to make a statement about the inapplicability of our current concepts of time and space to the universe, then proceed into the Standard Cosmological Model. These books often give the appearance of a straightforward methodological application of the prerequisite ideas. However, in general, in my experience, they usually leave a burning question or two in the mind of the reader which goes unanswered.

The following is a short list of books, websites, and articles consistent with Milne's Model. The Litmus test of whether an idea is consistent or inconsistent with Milne's Model is to ask whether it attempts to apply Lorentz Transformations on a cosmological scale. If it does, it may be compatible with Milne's Model. If it does not, or suggests that doing so is somehow invalid, it may be compatible with the SCM.

Gravitation, Relativity and World Structure

I have only recently discovered A. E. Milne's book and it may take years for me to fully grasp everything in it. Only content from the first few chapters is given here. I feel fairly certain that he never changed his attitude toward the Einstein Field Equations, even though Robertson or Walker supposedly adopted much of his methodology in solving them. With all of the books on cosmological models available, I think this one has simply been overlooked.

Relativity Visualized

A much acclaimed title among laypersons, and much maligned among cosmology experts, Lewis Carroll Epstein’s 1976 work, Relativity Visualized, presents many of the same concepts presented by Milne. Having not sat through numerous arguments with Eddington, Russell, Einstein, etc, Epstein's work is much less argumentative.

Epstein's main goal was to explain the Theory of Relativity in a manner that was self-consistent and that *anyone* could understand. Even so, because of the difficulty of the two different coordinate systems presented, I would recommend that experts in the field should definitely read the Appendix before delving into the meat of the book. Epstein's description of a mixed coordinate system in his appendix is precisely that described by Milne in sections 60-64.

Epstein elected to self-publish a book with NO references whatsoever, which I have long found to be curious, but now see to be a point in its favor, since books which make slow methodological progress between the Special and General theory of relativity seem far and few between. The description and Illustration of the General Theory in Epstein's book is truly unique, and if the mathematics of the Schwarzschild Metric could be somehow illustrated by the nonmathematical models of Epstein, a great leap forward could be made in pedagogy.

I spoke to Lewis Epstein personally, who was not aware of Milne's work, but asked me if I knew a simple experiment available to distinguish with certainty whether the universe is described by Milne's Model, or by the phenomenon of expanding space. I admitted that I did not know of such an experiment, and he also did not know. I can only point to the simplicity of Milne's Model, and the fact that it does not predict Dark Matter, Dark Energy, etc., and many of the other advantages I have pointed out here.

Epstein views his own model as simply a self-consistent possibility, and has very little interest in holding it up as in any way "better" than the standard cosmological model, although he does recognize that it is distinct from the concept of "expanding space."

Website: Relativistic Flight through Stonehenge

The Relativistic Flight through Stonehenge is a very good source for giving an idea what to expect visually from objects moving toward us near the speed of light. These objects would appear elongated and would appear to me moving superluminally. Also, they would appear further away.

The diagrams clearly indicate that when the observer accelerates toward a stationary object, it appears further away. Extrapolation of this idea leads to the realization that this change in perceived distance is unlimited. This is yet another description the root cause of inflation using the assumption of Milne's Model.

How would you approach the problem of predicting this? My suggestion (warning--complex algorithm ahead): Define the coordinates in space and time of the event of light leaving the surface of the object you are observing. Perform a Lorentz Transformation on that event to find that event's new location in space and time. Assume that light travels in a sphere from that source, and the edge of the sphere is at the eye of the observer. The observed size and location of the object is at the precise center of that sphere.

CADO: Current Age of Distant Objects

Mike Fontenot had a research paper published on the topic of the Current Age of Distant Objects, which is consistent with the Milne Model, (and in particular the explanation for Inflation.) He determined that by accelerating toward a distant receding object, you increase its coordinate distance until you've matched pace with it, and cause its current coordinate age to change rapidly by accelerating toward or away from it.

RelLab

RelLab is a software simulation program for Macintosh designed to simulate the Special Theory of Relativity. This program is capable of accurate applications of the Special Theory of Relativity at any scale, without use or mention of Friedmann’s scale factor, which makes it compatible for doing rudimentary simulations of Milne’s model.

JDoolin 20:27, 16 August 2006 (UTC)