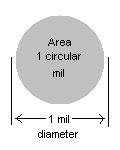
Circular mil
| circular mil | |
|---|---|
 | |
| General information | |
| Unit of | Area |
| Symbol | cmil |
| Derivation | 1 cmil = π/4(0.001 in)2 |
| Conversions | |
| 1 cmil in ... | ... is equal to ... |
| SI units | 506.7075 μm2 |
| FPS units | 7.853982×10−7 in2 |
A circular mil is a unit of area, equal to the area of a circle with a diameter of one mil (one thousandth of an inch or 0.0254 mm). It is equal to π/4 square mils or approximately 5.067×10−4 mm2. It is a unit intended for referring to the area of a wire with a circular cross section. As the definition of the unit contains π, it is easy to calculate area values in circular mils when the diameter in mils is known.
The area in circular mils, A, of a circle with a diameter of d mils, is given by the formula:
In Canada and the United States, the Canadian Electrical Code (CEC) and the National Electrical Code (NEC), respectively, use the circular mil to define wire sizes larger than 0000 AWG. In many NEC publications and uses, large wires may be expressed in thousands of circular mils, which is abbreviated in two different ways: kcmil[1] or MCM.[2] For example, one common wire size used in the NEC has a conductor diameter of 0.5 inches, or 500 mils, and thus a cross-section of circular mils, written as 250 kcmil or 250 MCM, which is the first size larger than 0000 AWG used within the NEC.
1,000 circular mil equals approximately 0.5067 mm2, so for many purposes, a ratio of 2 MCM ≈ 1 mm2 can be used with negligible (1.3%) error.
Equivalence to other units of area
[edit]As a unit of area, the circular mil can be converted to other units such as square inches or square millimetres.
1 circular mil is approximately equal to:
- 0.7854 square mils (1 square mil is about 1.273 circular mils)
- 7.854 × 10−7 square inches (1 square inch is about 1.273 million circular mils)
- 5.067 × 10−10 square metres
- 5.067 × 10−4 square millimetres
- 506.7 μm2
1000 circular mils = 1 MCM or 1 kcmil, and is (approximately) equal to:
- 0.5067 mm2, so 2 kcmil ≈ 1 mm2 (a 1.3% error)
Therefore, for practical purposes such as wire choice, 2 kcmil ≈ 1 mm2 is a reasonable rule of thumb for many applications.
Square mils
[edit]In square mils, the area of a circle with a diameter of 1 mil is:
By definition, this area is also equal to 1 circular mil, so
The conversion factor from square mils to circular mils is therefore 4/π cmil per square mil:
The formula for the area of an arbitrary circle in circular mils can be derived by applying this conversion factor to the standard formula for the area of a circle (which gives its result in square mils).
Square inches
[edit]To equate circular mils with square inches rather than square mils, the definition of a mil in inches can be substituted:
Square millimetres
[edit]Likewise, since 1 inch is defined as exactly 25.4 mm, 1 mil is equal to exactly 0.0254 mm, so a similar conversion is possible from circular mils to square millimetres:
Example calculations
[edit]A 0000 AWG solid wire is defined to have a diameter of exactly 0.46 inches (11.68 mm). The cross-sectional area of this wire is:
Formula 1: circular mil
[edit]Note: 1 inch = 1000 mils
(This is the same result as the AWG circular mil formula shown below for n = −3)
Formula 2: square mil
[edit]Formula 3: square inch
[edit]Calculating diameter from area
[edit]When large diameter wire sizes are specified in kcmil, such as the widely used 250 kcmil and 350 kcmil wires, the diameter of the wire can be calculated from the area without using π:
We first convert from kcmil to circular mil
Thus, this wire would have a diameter of a half inch or 12.7 mm.
Metric equivalent
[edit]Some tables give conversions to circular millimetres (cmm).[3][4] The area in cmm is defined as the square of the wire diameter in mm. However, this unit is rarely used in practice. One of the few examples is in a patent for a bariatric weight loss device.[5]
AWG circular mil formula
[edit]The formula to calculate the area in circular mil for any given AWG (American Wire Gauge) size is as follows. represents the area of number AWG.
For example, a number 12 gauge wire would use :
Sizes with multiple zeros are successively larger than 0 AWG and can be denoted using "number of zeros/0"; for example "4/0" for 0000 AWG. For an /0 AWG wire, use
- in the above formula.
For example, 0000 AWG (4/0 AWG), would use ; and the calculated result would be 211,600 circular mils.
Standard sizes
[edit]Standard sizes are from 250 to 400 in increments of 50 kcmil, 400 to 1000 in increments of 100 kcmil, and from 1000 to 2000 in increments of 250 kcmil.[6]
The diameter in the table below is that of a solid rod with the given conductor area in circular mils. Stranded wire is larger in diameter to allow for gaps between the strands, depending on the number and size of strands.
| Area | Diameter | NEC copper wire ampacity with 60/75/90 °C insulation (A)[7] | ||||
|---|---|---|---|---|---|---|
| (kcmil, MCM) |
(mm2) | (in) | (mm) | |||
| 250 | 126.7 | 0.500 | 12.70 | 215 | 255 | 290 |
| 300 | 152.0 | 0.548 | 13.91 | 240 | 285 | 320 |
| 350 | 177.3 | 0.592 | 15.03 | 260 | 310 | 350 |
| 400 | 202.7 | 0.632 | 16.06 | 280 | 335 | 380 |
| 500 | 253.4 | 0.707 | 17.96 | 320 | 380 | 430 |
| 600 | 304.0 | 0.775 | 19.67 | 355 | 420 | 475 |
| 700 | 354.7 | 0.837 | 21.25 | 385 | 460 | 520 |
| 750 | 380.0 | 0.866 | 22.00 | 400 | 475 | 535 |
| 800 | 405.4 | 0.894 | 22.72 | 410 | 490 | 555 |
| 900 | 456.0 | 0.949 | 24.10 | 435 | 520 | 585 |
| 1000 | 506.7 | 1.000 | 25.40 | 455 | 545 | 615 |
| 1250 | 633.4 | 1.118 | 28.40 | 495 | 590 | 665 |
| 1500 | 760.1 | 1.225 | 31.11 | 520 | 625 | 705 |
| 1750 | 886.7 | 1.323 | 33.60 | 545 | 650 | 735 |
| 2000 | 1013.4 | 1.414 | 35.92 | 560 | 665 | 750 |
Note: For smaller wires, consult American wire gauge § Tables of AWG wire sizes.
See also
[edit]- Thou (length)
- Square mil
- IEC 60228, the metric wire-size standard used in most parts of the world.
- American Wire Gauge (AWG), used primarily in the US and Canada
- Standard Wire Gauge (SWG), the British imperial standard BS3737, superseded by the metric.
- Stubs Iron Wire Gauge
- Jewelry wire gauge
- Body jewelry sizes
- Electrical wiring
- Number 8 wire, a term used in the New Zealand vernacular
References
[edit]- ^ "Popular Acronyms" Archived 2011-09-03 at the Wayback Machine. NEMA
- ^ "Energy Acronyms", California Energy Commission
- ^ Charles Hoare, The A.B.C. of Slide Rule Practice, p. 52, London: Aston & Mander, 1872 OCLC 605063273
- ^ Edwin James Houston, A Dictionary of Electrical Words, Terms and Phrases, p. 135, New York: W. J. Johnston, 1889 OCLC 1069614872
- ^ Greg A. Lloyd, Bariatric Magnetic Apparatus and Method of Manufacturing Thereof, US patent US 8481076, 9 July 2013.
- ^ NFPA 70-2011 National Electrical Code 2011 Edition Archived 2008-10-15 at the Wayback Machine. Table 310.15(B)(17) page 70-155, Allowable Ampacities of Single-Insulated Conductors Rated Up to and Including 2000 Volts in Free Air, Based on Ambient Air Temperature of 30°C (86°F).
- ^ NFPA 70 National Electrical Code 2008 Edition Archived 2008-10-15 at the Wayback Machine. Table 310.16 page 70-148, Allowable ampacities of insulated conductors rated 0 through 2000 volts, 60°C through 90°C, not more than three current-carrying conductors in raceway, cable, or earth (directly buried) based on ambient temperature of 30°C. Extracts from NFPA 70 do not represent the full position of NFPA and the original complete Code must be consulted. In particular, the maximum permissible overcurrent protection devices may set a lower limit.






![{\displaystyle {\begin{aligned}\{A\}_{{\textrm {mil}}^{2}}&=\pi r^{2}=\pi \left({\frac {d}{2}}\right)^{2}={\frac {\pi d^{2}}{4}}&&({\text{Area in square mils}})\\[2ex]\{A\}_{\textrm {cmil}}&=\{A\}_{{\textrm {mil}}^{2}}\times {\frac {4}{\pi }}&&({\text{Convert to cmil}})\\[2ex]\{A\}_{\textrm {cmil}}&={\frac {\pi d^{2}}{4}}\times {\frac {4}{\pi }}&&({\text{Substitute area in square mils with its definition}})\\[2ex]\{A\}_{\textrm {cmil}}&=d^{2}.\end{aligned}}}](/media/api/rest_v1/media/math/render/svg/8b021bbee6e3e986140791736d8b607835ca3009)
![{\displaystyle {\begin{aligned}{\rm {1~cmil}}&={\rm {{\frac {\pi }{4}}~mil^{2}={\frac {\pi }{4}}~(0.001~in)^{2}}}\\[2ex]&={\rm {{\frac {\pi }{4{,}000{,}000}}~in^{2}\approx 7.854\times 10^{-7}~in^{2}}}\end{aligned}}}](/media/api/rest_v1/media/math/render/svg/5d59d67b43ff9a6c86856c8561149bb28fffdfb1)
![{\displaystyle {\begin{aligned}{\rm {1~cmil}}&={\rm {{\frac {\pi }{4}}~mil^{2}={\frac {\pi }{4}}~(0.0254~mm)^{2}={\frac {\pi \times 0.000\,645\,16}{4}}~mm^{2}}}\\[2ex]&={\rm {1.6129\pi \times 10^{-4}~mm^{2}\approx 5.067\times 10^{-4}~mm^{2}}}\end{aligned}}}](/media/api/rest_v1/media/math/render/svg/e2c5727a542cc508730fd5985f94eae393c8c4c7)












