Logarithmic scale

A logarithmic scale (or log scale) is a method used to display numerical data that spans a broad range of values, especially when there are significant differences among the magnitudes of the numbers involved.
Unlike a linear scale where each unit of distance corresponds to the same increment, on a logarithmic scale each unit of length is a multiple of some base value raised to a power, and corresponds to the multiplication of the previous value in the scale by the base value. In common use, logarithmic scales are in base 10 (unless otherwise specified).
A logarithmic scale is nonlinear, and as such numbers with equal distance between them such as 1, 2, 3, 4, 5 are not equally spaced. Equally spaced values on a logarithmic scale have exponents that increment uniformly. Examples of equally spaced values are 10, 100, 1000, 10000, and 100000 (i.e., 101, 102, 103, 104, 105) and 2, 4, 8, 16, and 32 (i.e., 21, 22, 23, 24, 25).
Exponential growth curves are often depicted on a logarithmic scale graph.


Common uses
[edit]The markings on slide rules are arranged in a log scale for multiplying or dividing numbers by adding or subtracting lengths on the scales.
The following are examples of commonly used logarithmic scales, where a larger quantity results in a higher value:
- Richter magnitude scale and moment magnitude scale (MMS) for strength of earthquakes and movement in the Earth

- Sound level, with the unit decibel
- Neper for amplitude, field and power quantities
- Frequency level, with units cent, minor second, major second, and octave for the relative pitch of notes in music
- Logit for odds in statistics
- Palermo Technical Impact Hazard Scale
- Logarithmic timeline
- Counting f-stops for ratios of photographic exposure
- The rule of nines used for rating low probabilities
- Entropy in thermodynamics
- Information in information theory
- Particle size distribution curves of soil

The following are examples of commonly used logarithmic scales, where a larger quantity results in a lower (or negative) value:
- pH for acidity
- Stellar magnitude scale for brightness of stars
- Krumbein scale for particle size in geology
- Absorbance of light by transparent samples
Some of our senses operate in a logarithmic fashion (Weber–Fechner law), which makes logarithmic scales for these input quantities especially appropriate. In particular, our sense of hearing perceives equal ratios of frequencies as equal differences in pitch. In addition, studies of young children in an isolated tribe have shown logarithmic scales to be the most natural display of numbers in some cultures.[1]
Graphic representation
[edit]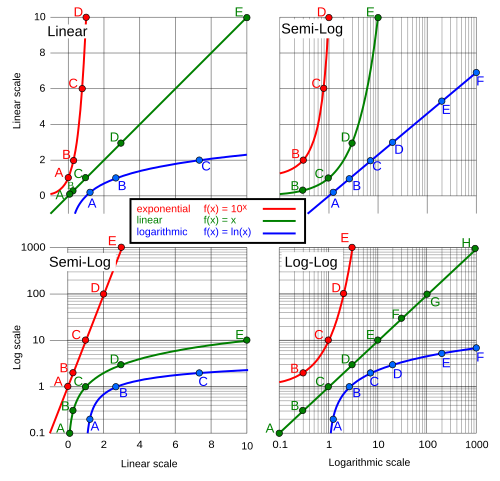
The top left graph is linear in the X- and Y-axes, and the Y-axis ranges from 0 to 10. A base-10 log scale is used for the Y-axis of the bottom left graph, and the Y-axis ranges from 0.1 to 1000.
The top right graph uses a log-10 scale for just the X-axis, and the bottom right graph uses a log-10 scale for both the X axis and the Y-axis.
Presentation of data on a logarithmic scale can be helpful when the data:
- covers a large range of values, since the use of the logarithms of the values rather than the actual values reduces a wide range to a more manageable size;
- may contain exponential laws or power laws, since these will show up as straight lines.
A slide rule has logarithmic scales, and nomograms often employ logarithmic scales. The geometric mean of two numbers is midway between the numbers. Before the advent of computer graphics, logarithmic graph paper was a commonly used scientific tool.
Log–log plots
[edit]
If both the vertical and horizontal axes of a plot are scaled logarithmically, the plot is referred to as a log–log plot.
Semi-logarithmic plots
[edit]If only the ordinate or abscissa is scaled logarithmically, the plot is referred to as a semi-logarithmic plot.
Extensions
[edit]A modified log transform can be defined for negative input (y < 0) to avoid the singularity for zero input (y = 0), and so produce symmetric log plots:[2][3]
for a constant C=1/ln(10).
Logarithmic units
[edit]A logarithmic unit is a unit that can be used to express a quantity (physical or mathematical) on a logarithmic scale, that is, as being proportional to the value of a logarithm function applied to the ratio of the quantity and a reference quantity of the same type. The choice of unit generally indicates the type of quantity and the base of the logarithm.
Examples
[edit]Examples of logarithmic units include units of information and information entropy (nat, shannon, ban) and of signal level (decibel, bel, neper). Frequency levels or logarithmic frequency quantities have various units are used in electronics (decade, octave) and for music pitch intervals (octave, semitone, cent, etc.). Other logarithmic scale units include the Richter magnitude scale point.
In addition, several industrial measures are logarithmic, such as standard values for resistors, the American wire gauge, the Birmingham gauge used for wire and needles, and so on.
Units of information
[edit]Units of level or level difference
[edit]Units of frequency level
[edit]Table of examples
[edit]| Unit | Base of logarithm | Underlying quantity | Interpretation |
|---|---|---|---|
| bit | 2 | number of possible messages | quantity of information |
| byte | 28 = 256 | number of possible messages | quantity of information |
| decibel | 10(1/10) ≈ 1.259 | any power quantity (sound power, for example) | sound power level (for example) |
| decibel | 10(1/20) ≈ 1.122 | any root-power quantity (sound pressure, for example) | sound pressure level (for example) |
| semitone | 2(1/12) ≈ 1.059 | frequency of sound | pitch interval |
The two definitions of a decibel are equivalent, because a ratio of power quantities is equal to the square of the corresponding ratio of root-power quantities.[citation needed][4]
See also
[edit]- Alexander Graham Bell
- Bode plot
- Geometric mean (arithmetic mean in logscale)
- John Napier
- Level (logarithmic quantity)
- Log–log plot
- Logarithm
- Logarithmic mean
- Log semiring
- Preferred number
- Semi-log plot
Scale
[edit]Applications
[edit]References
[edit]- ^ "Slide Rule Sense: Amazonian Indigenous Culture Demonstrates Universal Mapping Of Number Onto Space". ScienceDaily. 2008-05-30. Retrieved 2008-05-31.
- ^ Webber, J Beau W (2012-12-21). "A bi-symmetric log transformation for wide-range data" (PDF). Measurement Science and Technology. 24 (2). IOP Publishing: 027001. doi:10.1088/0957-0233/24/2/027001. ISSN 0957-0233. S2CID 12007380.
- ^ "Symlog Demo". Matplotlib 3.4.2 documentation. 2021-05-08. Retrieved 2021-06-22.
- ^ Ainslie, M. A. (2015). A Century of Sonar: Planetary Oceanography, Underwater Noise Monitoring, and the Terminology of Underwater Sound.
Further reading
[edit]- Dehaene, Stanislas; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008). "Log or linear? Distinct intuitions of the number scale in Western and Amazonian indigene cultures". Science. 320 (5880): 1217–20. Bibcode:2008Sci...320.1217D. doi:10.1126/science.1156540. PMC 2610411. PMID 18511690.
- Tuffentsammer, Karl; Schumacher, P. (1953). "Normzahlen – die einstellige Logarithmentafel des Ingenieurs" [Preferred numbers - the engineer's single-digit logarithm table]. Werkstattechnik und Maschinenbau (in German). 43 (4): 156.
- Tuffentsammer, Karl (1956). "Das Dezilog, eine Brücke zwischen Logarithmen, Dezibel, Neper und Normzahlen" [The decilog, a bridge between logarithms, decibel, neper and preferred numbers]. VDI-Zeitschrift (in German). 98: 267–274.
- Ries, Clemens (1962). Normung nach Normzahlen [Standardization by preferred numbers] (in German) (1 ed.). Berlin, Germany: Duncker & Humblot Verlag. ISBN 978-3-42801242-8.
{{cite book}}: ISBN / Date incompatibility (help) (135 pages) - Paulin, Eugen (2007-09-01). Logarithmen, Normzahlen, Dezibel, Neper, Phon - natürlich verwandt! [Logarithms, preferred numbers, decibel, neper, phon - naturally related!] (PDF) (in German). Archived (PDF) from the original on 2016-12-18. Retrieved 2016-12-18.
External links
[edit]- "GNU Emacs Calc Manual: Logarithmic Units". Gnu.org. Retrieved 2016-11-23.
- Non-Newtonian calculus website

